RSA (I) - Asymmetric Cryptography

Today I would like to talk to you about one of the most important asymmetric cryptographic algorithms in history: RSA.

Because of the algorithm complexity, I decided to divide this post in two parts. In the first one I will explain the algorithm and how the maths do their job here (don’t run away! They are not so complicated!). In the next part I will show you a real RSA implementation.

Rivest, Shamir and Adleman

RSA is an acronym for the names of its designers. This group of cryptologist and mathematicians from the MIT (Massachusetts Institute of Technology) made history when they published the first globally scalable asymmetric cryptographic algorithm, following the steps of Diffie-Hellman.

The maths

Although RSA’s maths are pretty easy, they rely on a couple of important theorems: Euler’s Theorem and Bezout’s Lemma.

Bezout’s Lemma asserts that, given two integers a and b, there exist x and y such that $a \cdot x + b \cdot y = GCD(a,b)$ .

More precisely, if a and b are relatively prime (their GCD is 1), then is true that: $a \cdot x + b \cdot y = 1$ .

Euler’s Theorem presents the Phi function, $\varphi (n)$ , which shows the amount of relatively primes numbers minor than n. If n is prime, then every minor number is relatively primer to n and, therefore, we can assert that $\varphi (n) = n-1$ . The theorem affirms that $a^{\phi (n)} \equiv 1 \mod(n)$ .

Moreover, when m and n are relatively primes, then $\varphi (n \cdot m) = \varphi (n) \cdot \varphi (m)$ .

Algorithm

RSA is slightly different from Diffie-Hellman. Whilst Diffie-Hellman relies on the discrete logarithm problem, RSA relies on the integer factorization problem: there is no algorithm capable of factoring large integers in a relatively short amount of time.

Imagine that Alice wants to send an encrypted message to Bob. To make it possible, Bob must perform some calculations…

Bob takes two random primes p and q, and he multiplies them, obtaining 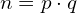$n = p \cdot q$ . The bigger the prime numbers, the more secure the implementation will be.
Now Bob takes $\varphi (n) = \varphi (p) \cdot \varphi (q)$ .
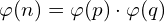Bob chooses a number e which will be the public key, relatively prime to 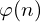$\varphi (n)$ . It is very common to choose the number 65537, since it is considered a “secure” prime. We can always choose the same number e, since we are working modulo n and n will be never repeated (because its random).
No Bob will get the private key, d, which will be the modular inverse of e, meaning he will look for a d such that 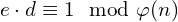$e \cdot d \equiv 1 \mod \varphi (n)$ . The Extended Euclidean Algorithm will let Bob perform this calculation efficiently.
Now Bob is able to share the pair (n,e) as his full public key, so Alice can send him encrypted messages.

At this moment, Alice has received Bob’s public key, so she sends him a message m.

Alice can get the encrypted message c like 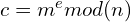$c = m^e mod(n)$ and send it to Bob.
Bob will receive the encrypted message c. To decrypt it, he can calculate $m = c^d mod(n)$ .

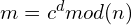Let’s pay special attention to the last step: when Bob receives the encrypted message c, what he really has is $c=m^e mod(n)$ . If he raises it to the private key, he will get $(m^e)^d mod(n)$ . Since e and d are inverses modulo $\varphi (n)$ means that $(m^e)^d mod (n) = m\ mod(n)$ . However, this step relies on a more complex argument, which I will explain at the end of the post.

What is really happening?

At this point, you may be asking Why is RSA so special?

If we take a closer look to the followed steps, we will see that the whole key has never been shared, only the public part. Only Bob has that special piece which allows the decryption of the message: his own private key, which has been never shared. This means that RSA’s security relies on keeping the private keys protected.

Imagine we are an attacker trying to intercept the message and decrypt it. We know Bob’s public key (n, e), because we intercepted it when he sent it to Alice. Can we get the original message?

The answer is no (if large and secure numbers have been used, of course). To decrypt the message, we should try every possible base m until we get c (which is ridiculous, since we will be brute-forcing the message itself). This would take a huge amount of time. The other way would be brute-forcing the private key, which could be even more difficult.

Problems

Although RSA is widely used, it is not perfect. Encrypting messages using RSA is slower than using symmetric algorithms like AES.

That is why RSA is used to encrypt symmetric keys and send them, so Alice and Bob can communicate using a faster symmetric algorithm. We call this hybrid cryptography.

Another problem is that RSA’s security relies on the fact that the integer factorization problem has not been solved yet. If someone discovered an efficient algorithm to factorize large integers, RSA would be easily broken in a short amount of time.

This why quantic computers are a real danger for cryptography. At the end of the 20th Century, Peter Shor designed an algorithm capable of factoring large numbers in a polynomial time, which means that RSA could be broken in some hours.

Although RSA is not really a complex algorithm, it is essential to pay special attention to its implementation. As an example, using short numbers or reusing modulus are important flaws that could allow an attacker to decrypt our communications.

Last step proof

As we mentioned when decrypting the message, we are going to prove the last step.

Why is it true that $(m^e)^d mod (n) = m$ ?

First, note that e and d are modular inverses modulo $\varphi (n) = (p-1) \cdot (q-1)$ , so we have $e \cdot d \equiv 1\mod \varphi (n)$ and, therefore there is a k such that $e \cdot d = k \cdot \varphi (n) + 1$ .

Now, let’s see that $(m^e)^d = m^{e \cdot d} = m^{k \cdot \varphi (n) + 1} = m^{k \cdot (p-1) \cdot (q-1)} \cdot m$ and following Euler’s Theorem we get $m^{p-1} \equiv 1\mod(p)$ y $m^{q-1} \equiv 1\mod(q)$ .

Finally, Chinese Reminder Theorem asserts that $m^{p-1} \equiv m^{q-1} \equiv 1\mod(n)$ . Therefore, $m^{k \cdot (p-1) \cdot (q-1)} \cdot m = 1^{(q-1) \cdot k} \cdot m \equiv m\mod(n)$ .

And that’s (not) all, folks! In the next post I will show an actual implementation of the algorithm using Python. Hope this one was not too dense!

Asymmetric Cryptography: RSA (I)